Introduction
BMI and body composition: theoretical considerations
Interpreting BMI in developed countries
Interpreting BMI in developing countries
Body composition of Third World populations and BMI
The effect of shape
References
Discussion
N. G. Norgan
Department of Human Sciences, Loughborough University, Loughborough, Leics LE 11 3TU, UK
This paper examines the
relationships between body mass index (BMI) and body composition in different population
groups where low BMIs might be expected to occur and assesses the extent to which BMIs are
influenced by size and shape. The relationship between BMI and fat as a percentage of body
weight is approximately linear although theoretically a curvilinear relationship is to be
expected. However, by allowing for a variable composition of weight differences, an
approximately linear theoretical relationship is obtained. There are few direct data (e.g.
from densitometry, hydrometry etc.) on body composition in the groups in question and to
examine the relationships indirect data were used. The regression coefficients of fat-free
mass on BMI for 285 samples of Africans, people of Asian origin, Indo-Mediterraneans and
Pacific people were not significantly different in the various groups of each sex; % fat
on BMI was similarly related in four groups of women. Intercept terms were all
significantly different. Using the sitting height-to-stature ratio (SH/S) as an index of
body shape in 158 groups, the regression coefficient of BMI on SH/S was 0.90 kg/m2
per 0.01 SH/S. Mean SH/S lies between 0.50 and 0.55 in most populations so that shape
could affect BMI by 5kg/m2 and influence markedly the interpretation of BMI.
However, allowing for SH/S is not straightforward as there is as much variation within as
between groups. In conclusion, low BMI approximates to low weight, fat mass and fat-free
mass. There are differences in the relationships of BMI to body composition but over the
range 20-25 kg/m2 these may not be important in epidemiological studies. To
interpret BMI in terms of body composition in more detail it is necessary to take into
account sex, age, shape and ethnicity.
Body weight and height are two simple anthropometric
measurements fundamental to a physical description of an individual or population. Both
measurements possess the virtues of being precise (highly repeatable), accurate (close to
the true value) and valid (representing what they are thought to represent). By themselves
they provide useful information on the mass and size of the human body. It has been
proposed that together they provide information on the composition of the body,
particularly the adiposity of the body. As different levels of fatness and energy stores
in an individual or population are associated with different levels of morbidity and
mortality, there is a need for a simple, non-invasive method for assessing fatness and
energy stores. This need has been the impetus to the investigation and use of weight:
height indices in nutrition. Body mass index (BMI; weight/height2, kg/m2),
has become the index of choice as it is more highly correlated with % fat and less well
correlated with stature than other weight: height indices.
If individuals and populations were of similar shape and composition, mass would be proportional to height cubed (H3). This is rarely observed in practice. Different exponents have been found in different populations for reasons that are not altogether clear. The implication of an exponent of 2 or close to 2 rather than 3 is that individuals range from the short and broad to the tall and narrow.
This paper examines the
relationships between BMI and body composition in different populations where low BMIs
might be expected. The extent to which low BMIs are influenced by differences in size and
shape is also assessed. There are meagre data on BMI and measured body composition in
Third World populations and the more voluminous data are indirect. The paper concludes
with a description of the contribution of variations in shape to BMI differences within
and between populations.
In the first instance, the relationship between BMI
and body composition can be modelled. Figure 1 shows the relationship when weight of
varying composition is added or subtracted to a 70 kg man of stature 1.75 m, i.e. with a
BMI of 22.9kg/m: and an assumed % fat of 15%. The relationship is non-linear and the slope
decreases as the proportion of fat in the weight difference falls. The BMI at 0% fat
varies too, ranging from 10 to 20kg/m2. There is an equally wide range in % fat
at high or low BMI. In a 60 kg woman, stature 1.625 m, BMI 22.7 kg/m2 and % fat
25%, a similar pattern emerges except that at a weight change with 25% fat being deposited
or lost, the line is horizontal. However, most investigators find the empirical
relationship between BMI and % fat to be linear or almost so.
Forbes (1987) has suggested that the composition of tissue lost or gained varies according to the initial level of fatness. There is less fat in the tissue change at lower levels of initial fatness. This was based on the differences of 164 women of widely differing composition but of stature limited to 1.56-1.70 m. The effect of this on the representative man and woman described above is shown in Fig. 2. In the man the relationship is almost linear between BMI 18 and 30kg/m2. Below 18, BMI falls more quickly than % fat. In the woman, the line is located higher and above BMI 10kg/m2 does not exhibit any marked curvature. These relationships accord better with the empirical data (Womersley & Durnin, 1977; Norgan & Ferro-Luzzi, 1982; Garrow & Webster, 1985). At BMI 20kg/m2, % fat is 10% in men and 20% in women. At 13kg/m2, it is 3% in men and 10% in women. These models using Forbes' equation suggest more reasonable values for % fat at a low BMI than any of the other models considered. However, the origin of Forbes' equation should be borne in mind as it may not be applicable to men or populations of different size and shapes.

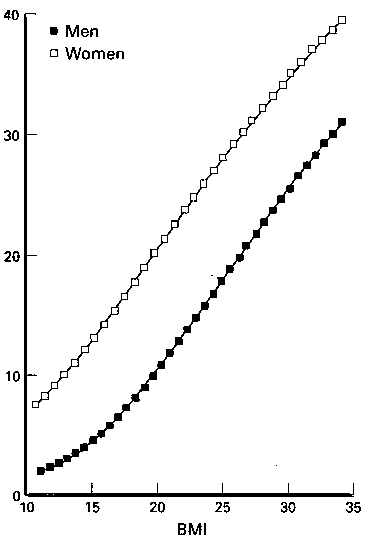
An example of the relationship between BMI and % fat
is given by a study of 138 Italian shipyard workers shown in Fig. 3. There was a
significant correlation between BMI and % fat, r = 0.75 (P < 0.001). The
performance of BMI as an estimator of fatness can be improved by allowing for age and sex
(Norgan & Ferro-Luzzi, 1982; Micozzi et al., 1986; Micozzi & Harris, 1990).
In these men, the multiple correlation of % fat and BMI and age was 0.83 as opposed to
0.75 for BMI alone. Other studies indicate that BMI explains about half the variation in %
fat (Garrow & Webster, 1985; Allen et al., 1956; Keys et al., 1972;
Roche et al., 1981; Revicki & Israel, 1986; Smalley et al., 1990;
Deurenberg, Westrate & Seidell, 1991). Although this is less than for skinfolds, which
on average explains 60-65% of the variation (Norgan, 1991), this is not always so. Here
the correlation of the sum of 4 skinfolds with % fat was 0.78.
What is particularly informative is
that BMI is more highly correlated with fat mass (FM), r = 0.87, than with % fat, r
= 0.75 and that BMI is highly correlated with measures of leanness, i.e. fat-free mass
(FFM), r = 0.68, and arm and thigh muscle circumferences, r= 0.78 and 0.81.
Strangely, limb circumferences, uncorrected for fatness were even more highly correlated, r
= 0.83-0.91. The explanation for this may be that the more specific or meaningful
measures of body composition such as limb muscle circumferences are measured less reliably
than the simple limb circumferences (Micozzi, 1990). However, BMI and weight:height
indices in general are as much measures of size as of composition and as much measures of
leanness as of fatness. The interpretation of BMI in terms of body composition can be
expected to vary in populations with different sizes and shapes.
In an earlier paper on this topic (Norgan, 1990),
the precise relationships between BMI and energy stores in developing countries could not
be identified because of shortage of data. A modelling approach similar to that used above
raised the possibility of very different body composition in different population groups
for the same BMI. This was based on assuming a % fat in groups of Papua New Guinea, Indian
and Ethiopian adults and, on the basis of their measured weights and heights, calculating
the effects of adding or subtracting tissue of known and constant composition. Changing
the assumptions about the initial level of fatness or the composition of the gain did not
alter the relative differences between the groups in terms of their varying composition at
a given BMI. The model predicted a curvilinear relationship between % fat and BMI but all
the empirical data showed a linear or almost linear trend. Possible reasons for this
difference were discussed. Further problems with the models were that the relationships
did not cover the known observed ranges of the variables. Zero % fat was predicted at BMI
>19 in some cases and 40% fat at BMI 30 was also interred. Altering the composition of
the gain could influence these values but only singly. Many of these problems can be
overcome if instead of adding or subtracting tissue of constant composition the
composition of gain is allowed to vary (Forbes, 1987), as suggested in the original paper.
Although the conclusions from the modelling exercise have been confirmed (Imminck, Flores
& Diaz, 1992), it requires further support from empirical data.